오늘은 백트래킹(Backtracking, 되추적) 알고리즘에 대해서 공부했다.
백트래킹 알고리즘이란 되추적이라고도 하는데 해를 구하기 위해 모든 경우의 수를 조사하지만 유망한 경우만 검사한다고 생각하면 된다. 흔히들 말하는 '가지치기'이다.
백트래킹은 DFS를 기반으로 만들어진다. 깊이 우선 탐색으로 인해 해당 경우의 수로 탐색하며 내려가다가 해당 노드가 조건에 맞지 않는다고 생각되면 가지치기하듯이 그 경우를 잘라내고 다시 상위 노드로 돌아가 다른 하위 노드로 내려가는 과정을 반복한다.
이를 위해 먼저 DFS를 알아두어야 한다.
백트래킹의 대표적인 예시로는 N-Queen 문제가 있는데 퀸을 어디에 놓느냐에 따라 다음 퀸을 놓을 수 있는 위치에 영향을 끼쳐 백트래킹 기법으로 검사를 하는 것이 가장 좋다.
N-Queen 문제는 N*N 체스판 위에 N개의 퀸을 놓음으로써 가능한 체스판의 경우의 수를 구하는 문제로 앞서 둔 말이 현재 말의 위치에 영향을 준다.
3*3 보드판이 있다고 가정하고 (0, 0)칸에 처음 퀸 말을 둔다고 가정하자.

이렇게 처음 칸에 말을 둔다면 다음으로 둘 수 있는 퀸은 어디에 있을까?
퀸이 같은 행, 같은 열, 대각선까지 범위를 가져 다음 말은 이전 퀸의 말과 다른 행, 다른 열, 다른 대각선에 위치해야 한다.
이 과정을 그림으로 그려본다면
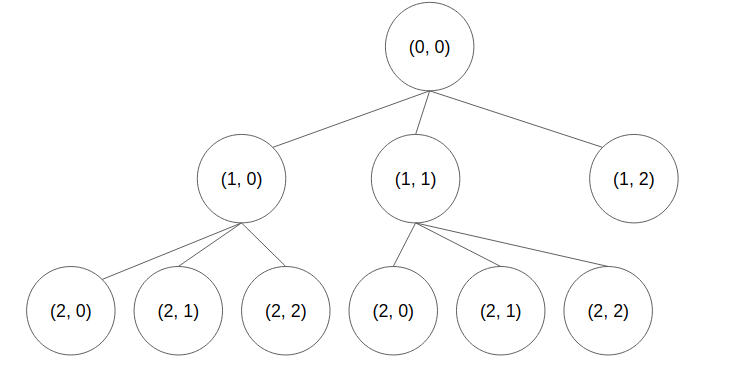
이런 식으로 그릴 수 있다. (편의상 (1, 2) 아래의 자식들은 생략했다.)
여기서 (1, 0)에 다음 말을 놓는 경우 (0, 0)에 놓았던 퀸의 열과 범위가 겹쳐 그 다음 말을 놓아보지 않아도 이 경우의 수는 조건에 부합하지 않는다는 것을 알 수 있다.
그럼 이 아래의 경우의 수는 볼 필요가 없으므로 가지치기를 진행해준다.
가지치기를 진행한후 다시 상위 노드로 돌아와 그다음 하위 노드는 조건에 부합하는지 검사해준다.
(1,1)에 놓는 경우도 앞서 두었던 (0, 0)의 퀸과 대각선 범위가 겹치므로 가지치기를 진행해준다.
이 역시도 가지치기를 진행한 후 다시 놓았던 말을 취소하고 (0, 0)으로 돌아와 다음 노드를 검사해준다.

이렇게 되면 마지막 노드인 (1, 2)에 놓는 경우의 수만 남는다.
(1, 2)에 말을 놓아보니 충돌하는 경우가 없다.
그럼 (1, 2)에 말을 두고 다시 그 하위 노드를 검사하면 된다.


이런 식으로 진행되는 것이 백트래킹 기법이고 백트래킹은 DFS를 기반으로 진행됨을 알 수 있다.
(실제 N-Queen문제를 풀다 보면 n이 2이거나 3인 경우는 해가 없음을 알 수 있지만
이 글에서는 편의상 n이 3인 경우를 예시로 했다.)
정리하자면 백트래킹은 DFS를 이용하여 하위 노드와 인접한 하위노드들을 깊게 탐색한 다음 하나라도 조건에 부합하지 않는다면 다시 상위 노드로 돌아와 다음 하위 노드를 검색한다.
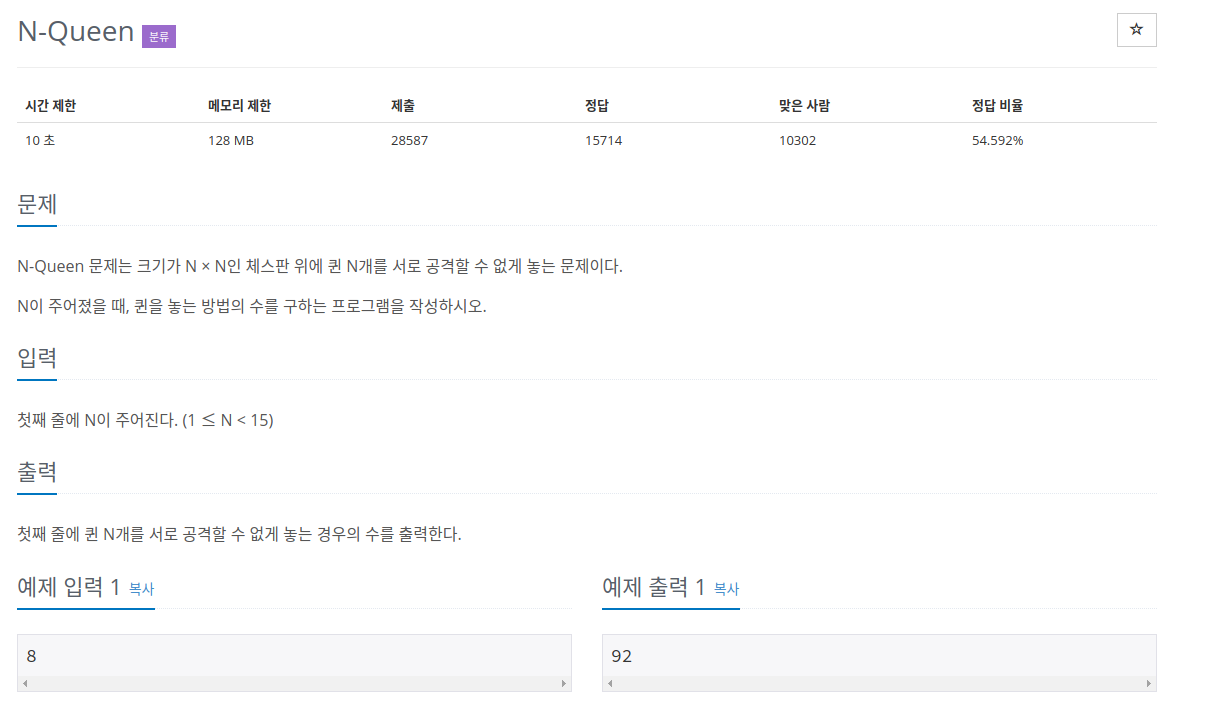
다음은 알고리즘 사이트로 유명한 백준에서 N-Queen문제이다.
// N-Queen
// node.js 에서 입력받기 위해 모듈 추가
let fs = require('fs');
let input = fs.readFileSync('/dev/stdin').toString().split(' ');
let num = Number(input); // 입력받은 숫자
let solution = 0; // 정답
let board = [];
// 이전에 둔 행을 돌면서 범위가 겹치는지 체크
function hasAnyQueensConflicts(x){
for(let i=0; i<x; i++){
if(board[i] === board[x]) { // 이전말과 같은 행 같은 열인지 체크
return true;
}
if(Math.abs(board[x] - board[i]) === x-i){ // 대각선 체크
return true;
}
}
return false;
}
// 재귀형태로 백트레킹기법 활용
function findNQueen(row){
if(row === num){
solution ++;
return;
}
for(let col=0; col<num; col++){
board[row] = col;
if(!hasAnyQueensConflicts(row)){ // 충돌 안한다면
findNQueen(row+1);
}
}
}
// 첫번째행을 넣고 실행
findNQueen(0);
console.log(solution);
이렇게 백트래킹 알고리즘 기법을 그의 대표적인 예시인 N-Queen으로 알아보았다.
백트래킹 기법을 사용하면 모든 경우의 수를 탐색하지 않아도 유망한 자식 노드만 검사 할 수 있으니 시간 복잡도가 훨씬 좋아진다.
'알고리즘 공부' 카테고리의 다른 글
| [JavaScript] DFS와 BFS에 대해서 (2) | 2020.11.05 |
|---|---|
| [C++] 삽입 정렬(Insertion sort) 알고리즘 (0) | 2020.09.14 |
| [C++] 이분 탐색(Binary Search) (0) | 2020.09.14 |
| [JavaScript] 소수 판별식 (6) | 2020.09.10 |

댓글